これは AmusementCreators 2020 アドベントカレンダー の 4日目の記事です。

こんにちは、檸檬茶です。 今回は、これまでの話とは一風変わって、巨大数のお話をしていこうと思います。 巨大数とは、読んで字の如くデカい数のことを指します。 数学には巨大数論(googology)という分野があり、いわゆる天文学的数字を遥かに上回る数について議論がなされているようです。 この分野では天文学の分野とは違い、巨大数は種々の特殊な記号で定義・表現されています。 この記事では、そんなありふれた学問にはまず登場しない数に、想いを馳せていきましょう。

とにかくデカい数字を書いてみよう

早速ですが皆さん、あなたが思うできる限りデカい数字を書いてみてください。 ただし、無限大や定義不可能な数を書くことを禁止とします。 ある人は9を書き連ねたり、あるいは無量大数(10の68乗)・グーゴル(10の100乗)・不可説不可説転(10の約37澗乗)といった数の単位を持ってくることでしょう。 あるいは指数に関する知識があるならば、9の9の9の…の9の9乗乗…乗乗といったように数字の右肩に9を書き連ねるかもしれません。 しかし残念ながら、そのような小手先のテクニックではより大きな数を表現することができません。 先述したとおり、巨大数論における巨大数は特殊な記号で定義・表現されています。 ではこれから、そのような記号について勉強していきましょう。

クヌースの矢印記法

巨大数を表現する一番簡単な方法を、クヌースの矢印記法を使うことです。 この表記法は、1976年にドナルド・クヌースによって確立されました。 そう、スタンフォード大学の数学者・計算機科学者で、The Art of Conputer Programing の著者であり LaTeX の開発者です。 そんなクヌースさんが考えた、巨大数を表す方法とは一体何なのか、順を追ってみてみましょう。

加算や乗算や冪乗は演算の繰り返しである

突然ですが加算や乗算や冪乗といった演算は、より低次の演算の繰り返しで表現することができます。
まず、加算はインクリメントの繰り返しです。 a+bはa+1+1+…をb回反復することで計算されます。 同様に、乗算は加算の繰り返しで、a×bはa+a+…をb回反復することで計算されます。 冪乗は乗算の繰り返しで、a↑bはa×a×…をb回反復することで計算されます。 つまり、インクリメントを繰り返すと加算、加算を繰り返すと乗算、乗算を繰り返すと冪乗という演算に変化するのです。
ここまで読んできた皆さんは「冪乗に使う記号は↑じゃなくて^じゃないのか」と疑問に思うかもしれません。 しかしこの表記法は、のちに説明する矢印記法の定義に深く関わってくるため、覚えておいてください。

冪乗を繰り返すと……?

では、冪乗を繰り返すとどのような演算になるのでしょうか? 冪乗の繰り返しということは、つまりこのように書き表されることになります。
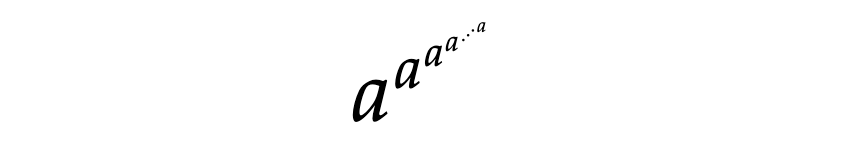この表記法を「指数タワー」と言い、このように冪乗の繰り返しを行う演算を「テトレーション」と言います。 これを使えば確かに巨大な数を表現することはできますが、より大きな数を表現したいために、同じ数を右肩に乗せ続けるのも腕が疲れます。 そこでクヌースさんは、このテトレーション演算を、二重矢印を使って次のように表現しました。
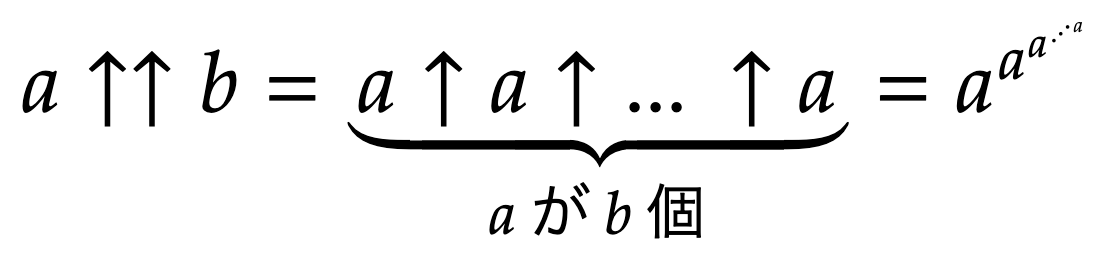この定義によると、例えば2↑↑4は次のように計算されます。
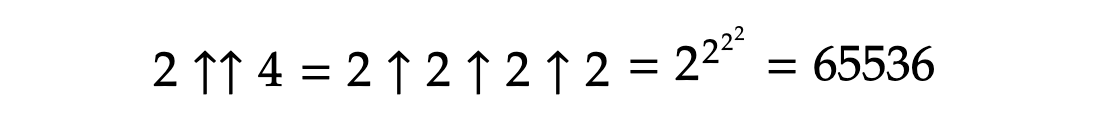同様に2↑↑5を計算すると2の65536乗、3↑↑4を計算すると3の7625597484987乗になると思います。 これだけでもすごい演算であることは嫌でも感じるでしょう。

矢印演算子の注意

矢印演算子は右結合です。必ず右から計算しましょう。

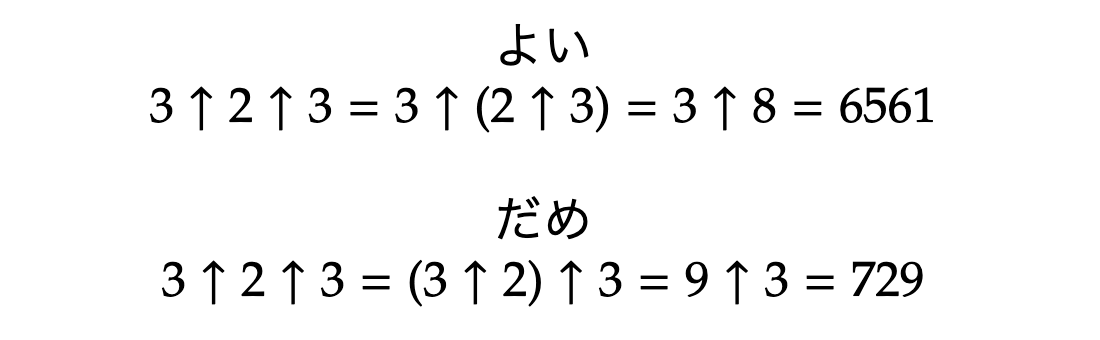
矢印記法の定義

ここまで矢印が1本の場合の演算、2本の場合の演算を紹介してきました。 クヌースの矢印記法の定義では、矢印がn本の場合にまで拡張されています。 その定義がこちらになります。ただし、矢印の右肩に乗っている数は矢印の本数を表しているものとします。
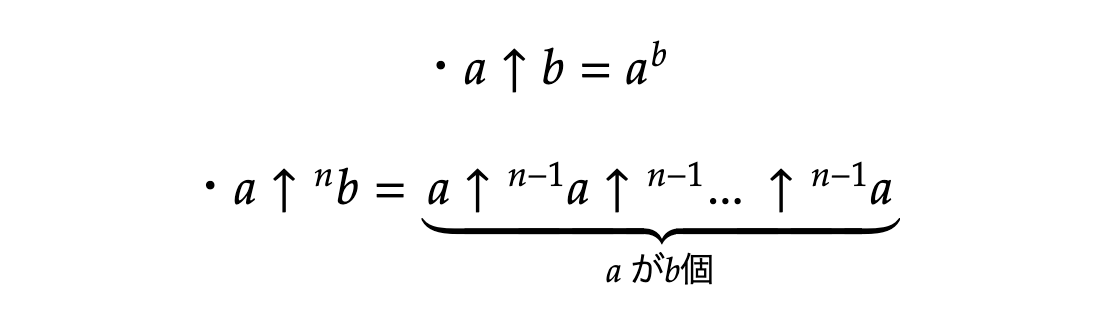では、この定義を使って3↑↑↑3を計算してみましょう。 これは「トリトリ」と呼ばれる巨大数です。 ちょっと嫌な予感はしますが、とりあえず計算してみましょう。 矢印演算子は必ず右から計算するというルールは、矢印が何本になっても同じです。
すなわちこの「トリトリ」と呼ばれる数は、3の3の3の…の3の3乗乗…乗乗が7625597484987個連なっているものになります。

わぁぉ。

でかい。

このような感じで、クヌースの矢印記法は、少ない記述量でとんでもなく大きな数字を表現する能力を持っています。 不可説不可説転なんてもはや0に等しいですね。(笑)

グラハム数

このクヌースの矢印記法を用いて表現されている有名な巨大数の一つに「グラハム数」があります。 グラハム数は「数学の証明に使用された最大の整数」として、ギネス世界記録に登録されています。 早速、グラハム数を計算してみましょう!
まず、関数g(x)を次のように定めます。
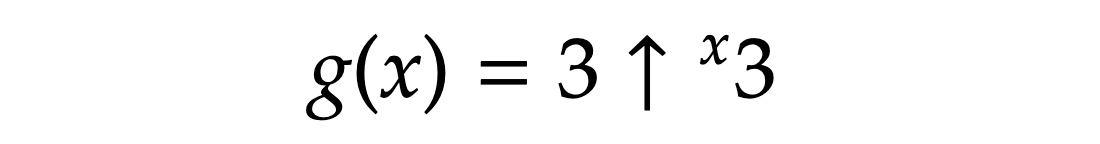
矢印の本数を変数化するとか気狂ってんだろ
x=3のとき、この関数の値は先ほど求めた「トリトリ」になります。 このように、xに適当な数字を入力してみると、とんでもなく大きな数が返ってきます。
次に関数gの引数に関数gの値を入力します。
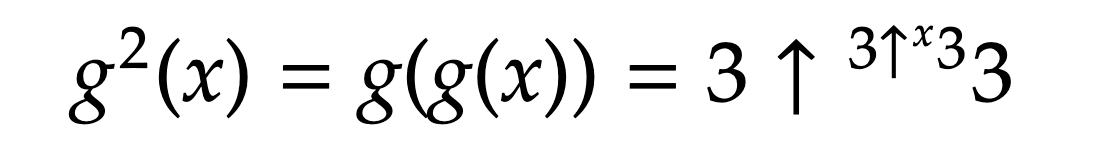こうすると、x=3のときg(x)の値はトリトリになって、矢印の本数がトリトリになるから……と考えただけでも恐ろしいですよね。 矢印の本数が一気に跳ね上がり、それだけ出力値もドカンと大きくなります。 このように、関数の出力値を次の入力値とする操作を何回も繰り返すことで、さらに大きな数を得ることができるというわけです。 いわゆる合成関数、関数の埋め込みですね。 この式について、g^n(x)のnはこの操作を反復した回数を表しているものとします。
では、これらを使ってグラハム数を表現すると、次のようになります!
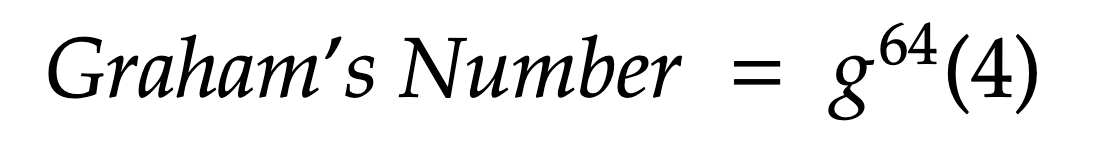
もうわけわかんねぇよ
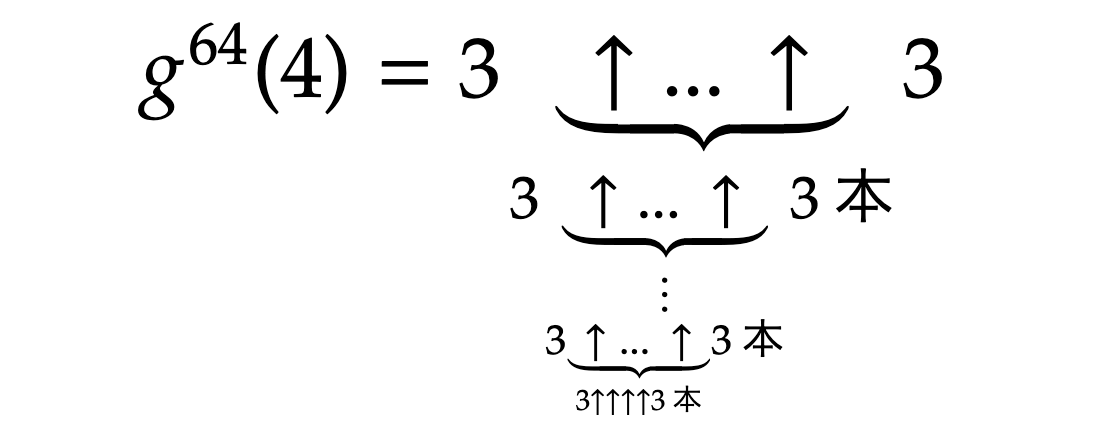
グラハム数では、関数の埋め込みを滅茶苦茶な数行ってるってことが見て取れますね。 これを矢印表記だけで無理矢理表そうとすると、こんな感じの階層構造が64段も連なっています。 もうわけわかんねぇよ(2回目)
こんな大きな数が実際の数学の証明で使われていたことは本当に驚きですね。
グラハム数は、クヌースの矢印記法のみを使ってギリギリ表すことのできる程度の数です。 これよりも大きな数を定義することはできますが、そのためにはより数が大きくなるような演算子を定義する必要があります。

最後に

いかがでしたでしょうか。 今回は巨大数論の最初の一歩について説明してきましたが、最初の一歩とは思えない大きさの数が登場して頭がいっぱいになってる方もいると思います。 自分も書いてて疲れました。(汗) これからもさまざまな巨大数、及びそれを表現するための定義を紹介していこうと思いますので、どうぞ最後までお付き合いください。 次は、アッカーマン関数について書く予定です。